Soal Latihan BOLA
HALAMAN 330, NO 2 dan 4
2. Diketahui titik P(2, 4, 5) dan menyinggung xy. Tentukan persamaan bola.
Pembahasan :
diketahui : r = 5
P(a, b, c) = P(2, 4, 5)
ditanya : persaamaan bola ?
jawab :
(x – a)2 + (y – b)2 + (z –
c)2 = r2
(x – 2)2 + (y – 4)2 + (z – 5)2 = 52
(x – 2)2 + (y – 4)2 + (z – 5)2 = 25
x2 + y 2 + z2 - 4x - 8y - 10z + 4 + 16 + 25 -25 = 0
x2 + y 2 + z2 - 4x - 8y - 10z + 20 = 0 (persamaan bola)
4. Tentuka pusat dan jari-jari bola dengan persamaan 4x2 + 4y 2 + 4z2 - 4x + 8y + 16z - 13 = 0
Pembahasan :
4x2 + 4y 2 + 4z2 - 4x + 8y + 16z - 13 = 0 (:4)
x2 + y 2 + z2 - x + 2y + 4z - 13/4 = 0
didapat : A = -1, B = 2, C = 4, D = -13/4
maka :
titik pusat bola adalah
Senin, 27 Mei 2019
BOLA
Devinisi Bola
Persamaan Bola
Devinisi Bola
Permukaan Bola merupakan tempat kedudukan titik ujung
vektor-vektor di dalam ruang yang titik awalnya adalah titik tertentu, dan
panjangnya adalah konstant.
Titik
awal tertentu itu disebut TITIK PUSAT Bola, dan panjang vektor yang konstant
itu disebut JARI-JARI Bola.Persamaan Bola
Persamaan bola dengan pusat P(a, b, c)
dan berjari-jari r. Ambil sembarang titik Q(x, y, z) pada bola.
(x – a)2 + (y – b)2
+ (z – c)2 = r2
KOORDINAT BOLA :
x² + y² + z² + Ax + By + Cz + D = 0
sehingga, didapat BENTUK UMUM persamaan Bola
-2a = A, maka a = -½ A
-2b = B, maka b = -½B
-2c = C, maka c = -½C
Dengan demikian pusat Bola B pada persamaan diatas adalah
M(-½A, -½B, -½C)
Begitu pula karena a² + b² + c² – R² = D, maka didapat jari-jari bola :
R² = a² + b² + c² – D
R² = (-½A)² + (-½B)² + (-½C)² – D
R² = ¼A² + ¼B² + ¼C² – D
R² = √(¼A² + ¼B² + ¼C² – D)
Untuk bola B dengan persamaan x² + y² + z² + Ax + By + Cz + D = 0 terdapat tiga kemungkinan, yaitu
1. Bila R² > 0, maka B adalah bola sejati
2. Bila R² = 0, maka B adalah bola titik (jari-jari = 0)
3. Bila R² < 0, maka B merupakan bola khayal
Minggu, 26 Mei 2019
ELLIPSE
Devinisi
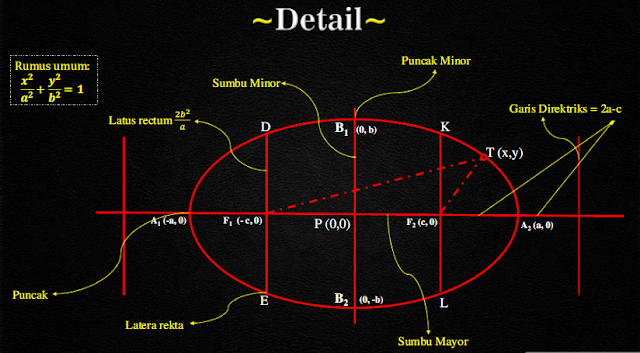
1) Elips yang berpusat di titik (0,0)
3) Garis
Singgung
Devinisi
Ellips adalah tempat kedudukan
titik-titik pada bidang datar yang jumlah jaraknya terhadap dua titik tertentu
yang diketahui adalah tetap/konstan.
1) Elips yang berpusat di titik (0,0)
Elips didefinisikan
sebagai lokus titik (x, y) yang bergerak sehingga jumlah jarak dari dua titik
tetap (disebut fokus, atau berfokus) adalah konstan. Jadi, persamaan yang digunakan pada elips saat titik focus berada di
(-a,0) dan (a,0) adalah
Dimana c didapat dari :
Jika sumbu utama adalah vertical, maka
rumusnya menjadi :
Kita selalu menggunakan a dan b seperti a
> b. Sumbu utama selalu dikaitkan dengan a.
HORIZONTAL :
VERTIKAL :
2) Elips
yang berpusat (h,k)
Untuk sumbu utama horizontal, jika bergerak
persimpangan sumbu x dan y ke titik (h,k) akan kita dapatkan:
HORIZONTAL :
VERTIKAL :
Garis singgung disuatu titik pada elips
yang membagi dua sama besar sudut antara garis penghubung.
Suatu garis lurus dapat memotong elips, menyinggung atau tidak memotong
dan tidak menyinggung elips. Dalam hal yang terakhri garis dan elips tidak
mempunyai titik persekutuan. Kita akan mencari persaman garis singgung yang
gradiennya m.
Jadi, persamaan garis singgung yang gradiennya m
adalah,
PARABOLA
Devinisi
Devinisi
Parabola adalah tempat kedudukan titik titik yang bergerak sama dari suatu
titik dan suatu garis tertentu. Titik itu disebut titik api
dan garis tertentu itu disebut garis garis arah (direktris).
Parabola adalah bagian kerucut yang merupakan irisan antara
permukaan suatu kerucut melingkar dengan suatu bidang datar. Parabola ini dapat
dinyatakan dalam sebuah persamaan:
Atau secara umum, sebuah parabola adalah kurva yang
mempunyai persamaan:
sehingga
dengan nilai A dan B yang
riel dan tidak nol.
Contoh
Tentukan
titik fokus dan garis direktris sebuah parabola y2
+ 10x = 0. Lalu buatlah sketsanya.
Pembahasan
:
y2
+ 10x = 0
y2
= -10x
puncak
di (0,0)
Selasa, 07 Mei 2019
HIPERBOLA DAN HIPERBOLOIDA
HIPERBOLA
Hiperbola diperoleh dari irisan kerucut. Hiperbola merupakan himpunan titik-titik pada suatu bidang yang selisih jaraknya terhadap dua titik tertentu besarnya sama.
Persamaan Hiperbola pusat (0, 0):
titik fokus pada sumbu-x
titik fokus pada sumbu-y
HIPERBOLOIDA
Hiperboloida merupakan himpunan titik-titik pada bidang tiga dimensi yang selisih jaraknya terhadap dua titik tetap adalah sama.
Persamaan Hiperboloida dua daun :
dengan mengatur setiap variabel sama dengan nol :
jejak pada bidang xy :
HIPERBOLA
(Perhatikan vidio di bawah ini!)
Hiperbola diperoleh dari irisan kerucut. Hiperbola merupakan himpunan titik-titik pada suatu bidang yang selisih jaraknya terhadap dua titik tertentu besarnya sama.
Persamaan Hiperbola pusat (0, 0):
titik fokus pada sumbu-x
titik fokus pada sumbu-y
HIPERBOLOIDA
(Perhatikan vidio di bawah ini!)
Persamaan Hiperboloida dua daun :
jejak pada bidang xy :
jejak pada bidang xz :
jejak pada bidang yz :
Langganan:
Postingan (Atom)